Der Physical Layer ist die Nahtstelle zur analogen Fading-Welt und die dabei zu bestimmenden Parameter sind gerade bei mobilen Teilnehmern oftmals sehr kurzzeitigen Änderungen unterworfen. Insofern ist eine Verbesserung der Parameterschätzung durch eine längere Lernzeit nicht möglich, sondern das Einfließen von zusätzlichen Informationen oder auch die Anwendung geeigneter Modelle müssen dann vorteilhaft eingesetzt werden.
Eine Anwendung ist die Bestimmung der aktuellen Verkehrslast, die sehr dynamisch sein kann. Dazu wurden Lösungsansätze entwickelt und erforscht, die zusätzliche Informationen einbinden [1], [2], [3], aber auch schneller konvergierende Algorithmen können erfolgreich eingesetzt werden [4].
Ein weiteres großes Thema ist die Erzeugung einer quasi-Reziprozität für Frequenzduplexsysteme (FDD-systems), um auch massive MIMO und time reversal Algorithmen mit diesen Systemen erfolgreich anwenden zu können. Dazu werden in der Abteilung Drahtlose Kommunikation und Netze verschiedene Forschungsansätze verfolgt [5], [6], [7], [8].
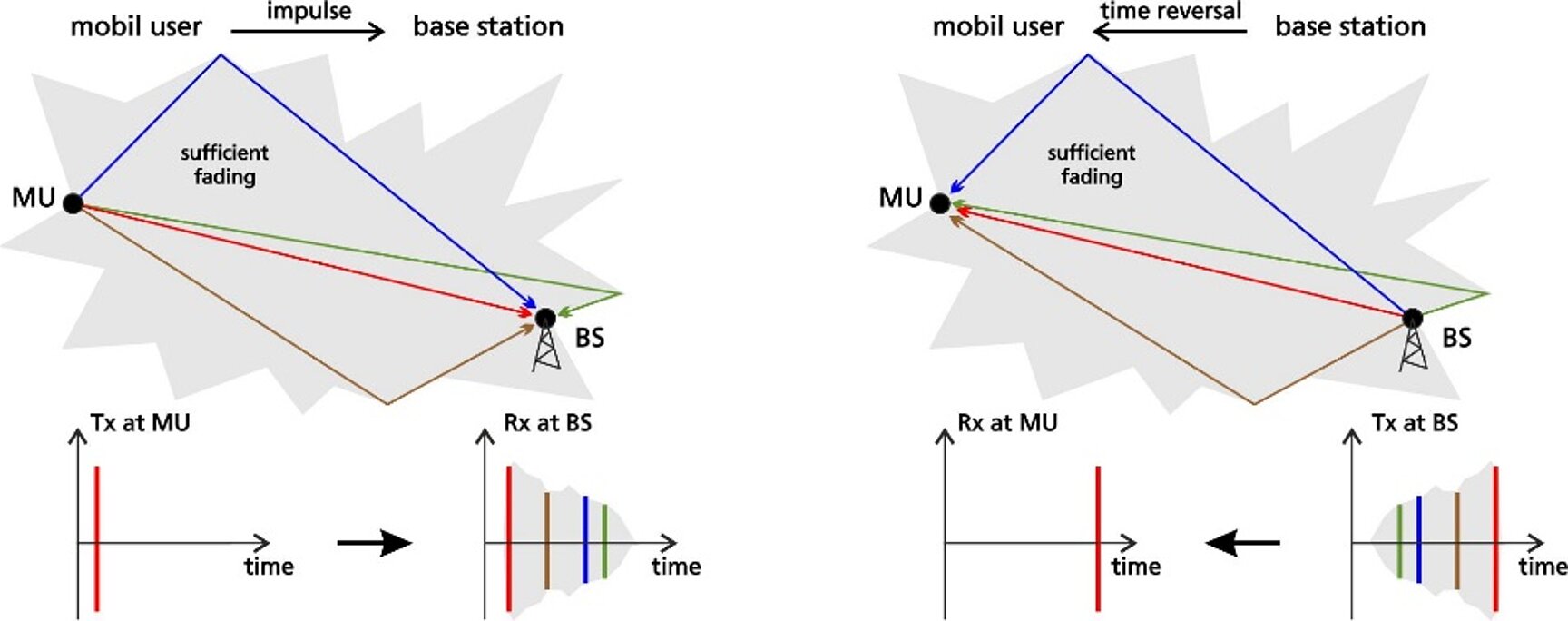
Das aktuelle Forschungsthema der Zeitumkehr (time reversal, siehe Abbildung) muss auch im physical layer etabliert werden, da dazu die Fading-Eigenschaften deutlich innerhalb der Kohärenzzeit bestimmt werden müssen. Nur dann kann das Empfangsmuster auch noch erfolgreich zur Festlegung des direkt folgenden Sendemusters verwendet werden. Bei genügend großem Fading ergibt dies eine sehr leistungs- und datenrateneffiziente Übertragung.
Weitere Forschungsarbeiten der Abteilung Drahtlose Kommunikation und Netze zur Anwendung des maschinellen Lernens im physical layer behandeln u. a.: Cell-less systems [9], nonlinear beamforming [10], Peak-to-average power ratio (PAPR) reduction [11], [12] und massive random access [13].
Referenzen
[1] D. A. Awan, R. L. G. Cavalcante, and S. Stańczak, "A robust machine learning method for cell-load approximation in wireless networks," in Proc. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Apr. 2018
[2] R. L. G. Cavalcante, Y. Shen, S. Stańczak, "Elementary Properties of Positive Concave Mappings with Applications to Network Planning and Optimization," IEEE Trans. Signal Processing, vol. 64, no. 7, pp. 1774-1783, April 2016
[3] R. L. G. Cavalcante, M. Kasparick, and S. Stańczak, "Max-min utility optimization in load coupled interference networks," IEEE Trans. Wireless Comm., vol. 16, no. 2, pp. 705-716, Feb. 2017
[4] D. A. Awan, R. L. G. Cavalcante, M. Yukawa, and S. Stańczak, "Detection for 5G-NOMA: An Online Adaptive Machine Learning Approach," in Proc. IEEE International Conference on Communications (ICC), May 2018
[5] R. L. G. Cavalcante, L. Miretti, and S. Stańczak, "Error bounds for FDD massive MIMO channel covariance conversion with set-theoretic methods," in Proc. IEEE Global Telecommunications Conference (GLOBECOM), Dec. 2018
[6] A. Decurninge, M. Guillaud, and D.T.M. Slock, “Channel covariance estimation in massive MIMO frequency division duplex systems,” in IEEE Globecom, 2015
[7] L. Miretti, R. L. G. Cavalcante, and S. Stańczak, "Downlink channel spatial covariance estimation in realistic FDD massive MIMO systems," IEEE Global Conference on Signal and Information Processing (GlobalSIP), 2018
[8] L. Miretti, R.L.G. Cavalcante and S. Stanczak, „FDD Massive Channel Spatial Covariance Using Projection Methods, in Proc. IEEE ICASSP, April 2018
[9] D. A. Awan, R. L. G. Cavalcante, Z. Utkovski, and S. Stanczak, “A set-theoretic method for detection in cell-less systems,” submitted
[11] J. Fink, R. L. G. Cavalcante, and S. Stańczak, “Extrapolated Projection Methods for PAPR reduction," submitted
[12] R. L. G. Cavalcante and I. Yamada, "A flexible peak-to-average power ratio reduction scheme for OFDM systems by the adaptive projected subgradient method,” IEEE Trans. Signal Processing, vol. 57, no. 4, pp. 1456-1468, April 2009
[13] P. Agostini, Z. Utkovski, J. Pilz, S. Stanczak, Scalable massive random access in C-RAN with fronthaul limitations, submitted